Data Completion

Introduction

In the modern world of big data, where we have access to a mind-boggling amount of information about all things, it might seem surprising that the vast majority of datasets are actually, overwhelmingly, incomplete (in one form or another). For example, consider the domain of collaborative filtering, where algorithms attempt to predict user preference(s) (i.e., a subset of incomplete data) using a selection of existing user data.

An infamous example of collaborative filtering in action is the Netflix problem, where Netflix offered a cash prize to develop the best collaborative filtering algorithm for predicting user film ratings. Historically, most Netflix users rated well below 1% of the company’s entire film catalogue, yet we can accurately predict individual user ratings for all films using only this small sampling. Generally, the problem of trying to “complete” a data set from a subset of known entries (i.e., data completion) is referred to as matrix (2-dimensional) or tensor (N-dimensional) completion. Collaborative filtering tasks, such as the Netflix problem, can often be solved by matrix or tensor completion programs. Indeed, low-rank matrix completion using alternating minimization comprised a major component of the winning Netflix prize entry.

Quantum State Completion

Project motivations: In quantum many-body physics, various sampling-based numerical schemes exist (e.g., quantum Monte Carlo) for characterizing quantum states. However, we can potentially improve certain methods by allowing them to “skip to the end” from a limited subset of known wavefunction coefficients (i.e., the values that define the quantum state), effectively revealing all of the unreliable or missing data points. This concept represents a data completion problem inside the Hilbert space of quantum wavefunctions. Here is a simple graphicial representation of what quantum completion might look like:

While solutions to this problem have worthy use-cases within computational quantum physics, they may also have interesting applications to other areas of data science. The interconnected nature between particles in many-body wavefunctions maps neatly onto many aspects of big data, and effective quantum completion algorithms are therefore likely to prove useful outside of physics as well (e.g., image completion; see results below).

Programming: While working as a graduate research scientist with Professor Glen Evenbly at Georgia Tech, I designed and programmed several novel algorithms for quantum state completion using Python and Matlab. In addition to developing solutions based on tensor network methods (e.g., randomly structured tensor trees, matrix product states), I also developed an independent solution using stacked convolutional neural networks with supervised learning. The latter represents a new use-case for AI and machine learning. Some of my findings are discussed in-depth in the article Reconstruction of Randomly Sampled Quantum Wavefunctions using Tensor Methods. Implementations of these methods and code demos are available in Python on my Github page. More extensive programs written in Matlab are available on request.

The figure below demonstrates the structure of one of my quantum completion algorithms. This method is applicable to finite quantum states on 1-D lattices with open boundary conditions. In lay terms, this method works well for quantum systems where the particles are distributed evenly along a straight line. In this approach, matrix product states are used to approximate the values of the missing wavefunction coefficients. Critically, (a) the approximate, or “trial”, wavefunction is anchored to the subset of randomly sampled coefficients (i.e., the known data points are fixed to their true values), and (b) the bond dimension \(\chi\) between the tensors comprising the matrix product state is sequentially incremented by 1 starting from the smallest non-trivial value (\(\chi=d\), where \(d\) is the local dimension of each lattice site).

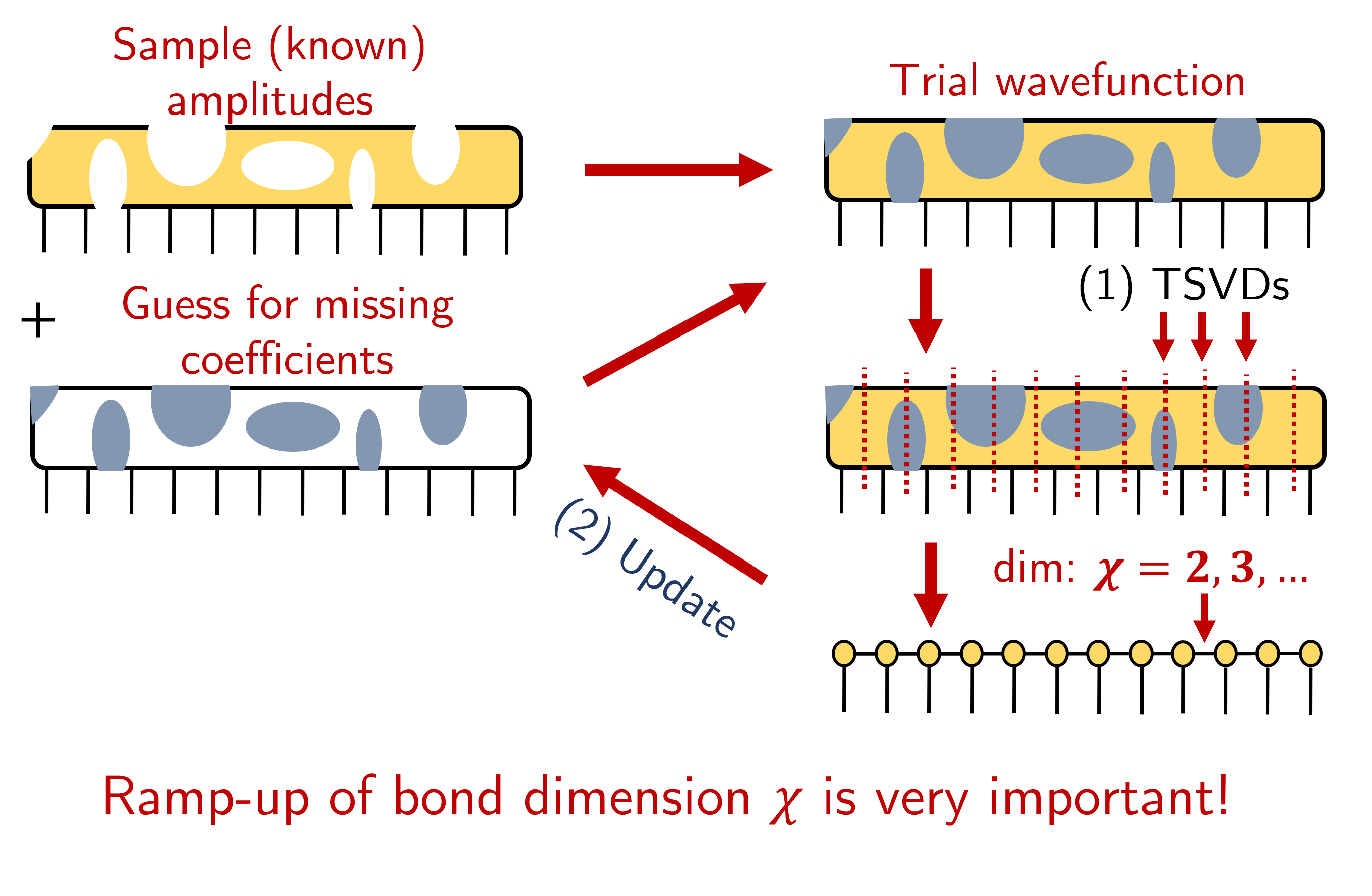The trial wavefunction (top-right) is initialized with the sum of a random sampling of wavefunction coefficient values (top-left) and an initial guess of zero for the missing or unknown coefficients (center-left). Next, the trial wavefunction is decomposed with truncated singular value decompositions (see (1) TSVD step) to form a matrix product state (bottom-right). This state is used to update the values of the missing coefficients (see (2) update step), which is then superposed with the known values to form a new trial wavefunction. The algorithm converges in each bond dimension \(\chi\), where \(\chi\) reflects the dimensionality between each tensor in the matrix product state, before it is incremented to the next bond dimension \(\chi=\chi+1\).

Results: Both the neural network and tensor network solutions for quantum wavefunction completion demonstrate attractive congergence properties and robust reliability. Low-energy quantum wavefunctions can be completed using either paradigm with near-perfect consistency given a sufficiently large random sample of known wavefunction coefficients. To see what this looks like in practice, consider the sequence of figures below :

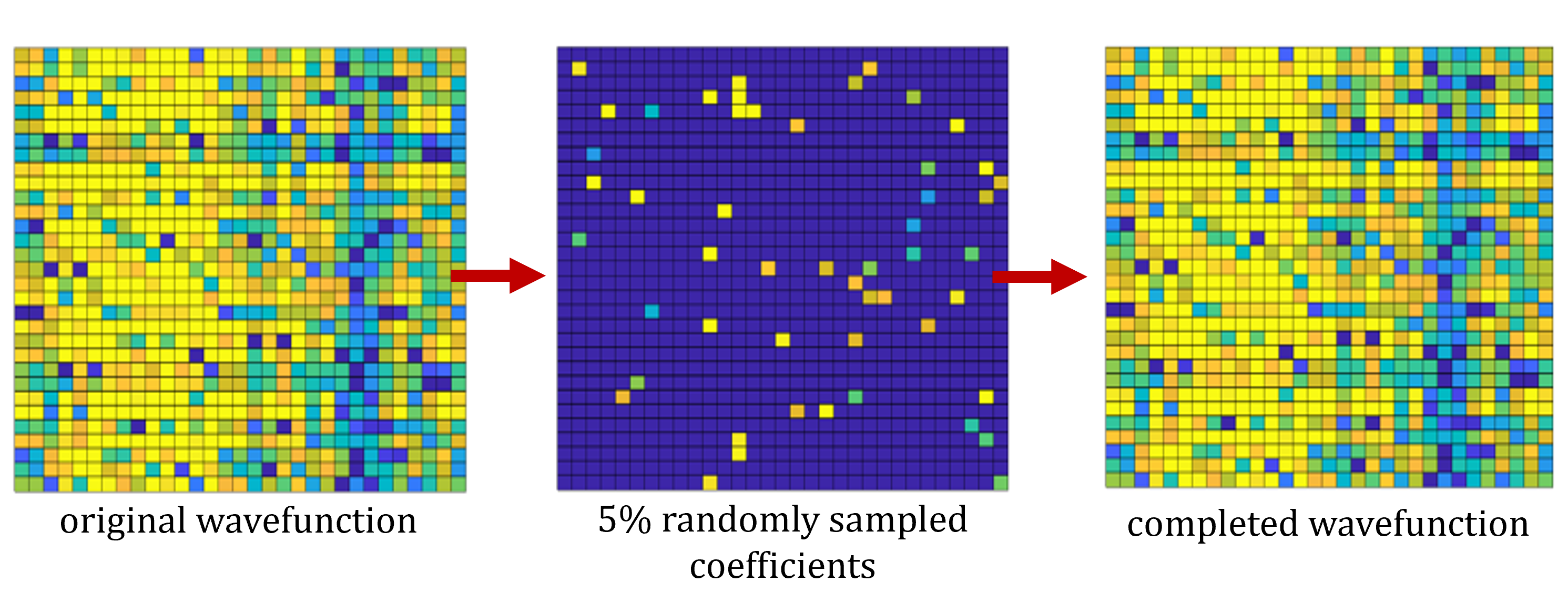
The three pictures above each display a 2-D representation of quantum wavefunction coefficient amplitudes. The true wavefunction (left image) is first calculated by performing an exact numerical diagonalization of the system’s Hamiltonian (see exactDiagEx.py for the code implementation). Next, 5% of the wavefunction coefficients are sampled (center image). Finally, the quantum completion routine is applied to restore (or “complete”) the missing coefficients (right image). From a human persepctive, it looks like there isn’t anywhere near enough information in the center panel to accurately complete the state (i.e., could you manually restore the state from just the sampling given in the middle panel?). This intuition is largely correct and therefore matrix completion algorithms, which restrict data to a fixed 2-D format as displayed here, do not effectively work on quantum states. In order to accurately recover the missing wavefunction values from such a small subset of coefficients, the completion program must utilize all non-trivial bipartitions of the state, performing truncated decompositions across each partition and updating the missing values accordingly.

Applications in Data Science

While working on this project, I became interested in deploying my quantum completion algorithms for conventional data science completion problems as well (e.g., image completion, where a subset of pixels are damaged or missing). By repurposes the algorithm to operate on 2-D images instead of N-D tensors, I was able to obtain some pretty cool and impressive results:

In this figure, the left panel represents the original, uncorrupted image; the central panel consists of a random sample of 10% of the pixels in the original image; and the right panel is the result of applying the repurposed quantum completion algorithm to the center image. Note: the left and right panels may appear identical, but close inspection reveals subtle differences. In developing this solution, I found that locally reshaping an image into more than two dimensions and then decomposing (i.e., truncated singular value decompositions) across these higher dimension provided additional information for missing pixels, allowing a more accurate image restoration. While the rudimentary adaptation of my algorithm is computationally inefficient relative to existing image completion routines, this tensor-based approach yields accuracies (e.g., PSNR, RMSE) that are competitive with the best existing methods. Research into quantum completion via neural and tensor networks is still in its infancy, but as I demonstrated here, it is a tractable problem and its solutions may have compelling use-cases in the broader arena of data science.